В предыдущих постах (раз, два, три) у нас шарики сталкивались друг с другом и отражались от границ, но теперь я решил добавить дополнительные препятствия в виде линий, от которых шарики будут отскакивать так же, как от границ - по "оптическому" закону. И если с вертикальными и горизонтальными границами все довольно просто - проверяешь не вышел ли обьект за границу x либо y компоненты и меняешь соответствующую компоненту скорости на противоположную (т.е. умножаешь на -1). А например в случае отражения шариков друг от друга мы просто сверяем расстояния между центрами шариков S с суммой их радиусов R1 + R2 и если S <= R1 + R2 то уже идет расчет новых векторов движения. Но в случае столкновения с протяженным обьектом все будет несколько иначе. Сначала надо представить центр шарика и два конца отрезка в виде треугольника:
- void checkCollision(const BorderLine& bl)
- {
- // rectangle around line
- Point2f xyMin = bl.getXYMin();
- xyMin = {xyMin.x - r, xyMin.y - r};
- Point2f xyMax = bl.getXYMax();
- xyMax = { xyMax.x + r, xyMax.y + r };
- if (pos.x >= xyMin.x && pos.y >= xyMin.y && pos.x <= xyMax.x && pos.y <= xyMax.y)
- {
- Point2f a = pos;
- // sides of triangle
- float p1a = bl.p1.distanceTo(a);
- float p2a = bl.p2.distanceTo(a);
- float p1p2 = bl.p1.distanceTo(bl.p2);
- // angles
- float ang1 = acos((p1a * p1a + p1p2 * p1p2 - p2a * p2a) / (2 * p1a * p1p2));
- float ang2 = acos((p2a * p2a + p1p2 * p1p2 - p1a * p1a) / (2 * p2a * p1p2));
- // if both angles are sharp then calculate h (distanse from a to line)
- if (ang1 <= k_PI / 2 && ang2 <= k_PI / 2)
- {
- float h = sin(ang1) * p1a;
- if (h <= r)
- {
- // calculate contact point
- float cath1 = cos(ang1) * p1a;
- Point2f v = (bl.p2 - bl.p1).unitVector() * cath1;
- Point2f contactPoint = bl.p1 + v;
- opticCollPoint(contactPoint);
- }
- }
- else if (p1a <= r)
- {
- opticCollPoint(bl.p1); // first line end
- }
- else if (p2a <= r)
- {
- opticCollPoint(bl.p2); // second line end
- }
- }
- }
- void opticCollPoint(const Point2f contactPoint)
- {
- // direction to other contact point
- Point2f toContPoint = contactPoint - pos;
- // calculate dot product
- float dotProd = f.dotProduct(toContPoint);
- // if dot product is negative then force directed away
- // from contact point and we do nothing
- if (dotProd > 0)
- {
- // angle between normal and force (moving) vectors
- float angle = f.angleTo(toContPoint);
- // the angle of incidence is equal to the angle of reflection
- f = Mat2x2f().rot(angle * 2) * f;
- f = f * (-1.f);
- }
- }
- Ball opticCollPoint(Ball b, float2 contactPoint)
- {
- float2 pos = (float2)(b.pos.x, b.pos.y);
- // direction to other contact point
- float2 toContPoint = contactPoint - pos;
- // calculate dot product
- float2 f = (float2)(b.f.x, b.f.y);
- float dotProd = dot(f, toContPoint);
- // if dot product is negative then force directed away
- // from contact point and we do nothing
- if (dotProd > 0)
- {
- // angle between normal and force (moving) vectors
- float angle = getAngleTo(f, toContPoint);
- // the angle of incidence is equal to the angle of reflection
- f = rotVect(f, angle * 2);
- f = f * (-1);
- b.f.x = f.x;
- b.f.y = f.y;
- }
- return b;
- }
- Ball checkCollisionBL(Ball b, BorderLine bl)
- {
- // rectangle around line
- Point2f xyMin = getBLXYMin(bl);
- xyMin.x = xyMin.x - b.r;
- xyMin.y = xyMin.y - b.r;
- Point2f xyMax = getBLXYMax(bl);
- xyMax.x = xyMax.x + b.r;
- xyMax.y = xyMax.y + b.r;
- if (b.pos.x >= xyMin.x && b.pos.y >= xyMin.y && b.pos.x <= xyMax.x && b.pos.y <= xyMax.y)
- {
- float2 a = (float2)(b.pos.x, b.pos.y);
- // sides of triangle
- float2 blp1 = (float2)(bl.p1.x, bl.p1.y);
- float2 blp2 = (float2)(bl.p2.x, bl.p2.y);
- float p1a = getDistanceBetween(blp1, a);
- float p2a = getDistanceBetween(blp2, a);
- float p1p2 = getDistanceBetween(blp1, blp2);
- // angles
- float ang1 = acos((p1a * p1a + p1p2 * p1p2 - p2a * p2a) / (2 * p1a * p1p2));
- float ang2 = acos((p2a * p2a + p1p2 * p1p2 - p1a * p1a) / (2 * p2a * p1p2));
- // if both angles are sharp then calculate h (distanse from a to line)
- if (ang1 <= M_PI_2_F && ang2 <= M_PI_2_F)
- {
- float h = sin(ang1) * p1a;
- if (h <= b.r)
- {
- // calculate contact point
- float cath1 = cos(ang1) * p1a;
- float2 v = (blp2 - blp1);
- v = getUnitVector(v) * cath1;
- float2 contactPoint = blp1 + v;
- b = opticCollPoint(b, contactPoint);
- }
- }
- else if (p1a <= b.r) // first line end
- {
- b = opticCollPoint(b, blp1);
- }
- else if (p2a <= b.r) // second line end
- {
- b = opticCollPoint(b, blp2);
- }
- }
- return b;
- }


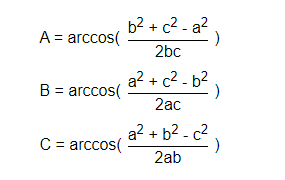
Комментариев нет:
Отправить комментарий